Password Policy Attacking Costs, part 1: Theory and Results
- By Miloslav Homer
- Sun 10 March 2024
- Updated on Fri 14 June 2024
The humble password needs no introduction. It's an essential security tool: I know this secret/text/code, you don't. Therefore, my stuff is secure unless you figure out this string of characters. Password policy is a similarly famous concept. To ensure your password is strong, follow these simple rules (or not so simple - check out this funny game).
But what exactly does this mean for an attacker? Can we measure the attacker’s effort in dollars? I have an idea.
This article is the first part containing the theory and main results, free from technical issues and ranting. If you are interested in those, check out part 2
If you already have the basics of passwords and cracking down, feel free to skip to Renting GPUs and The Cost of Time. If you trust that I got the data correct (check out the source code), feel free to skip to Policy Complexity Calculations to see the conclusions. Moreover, I then run an experiment to verify I've got the calculations approximately correctly (there's some overhead and whatnot in the end).
Password Storing Basics
If nobody ever told you:
DO NOT STORE PLAIN PASSWORDS ANYWHERE!
Of course, there are caveats, the most notable being the password manager.
That being said, use a hash function with salt.
Salt is a small random value that you generate when setting the password for the first time. Append this salt to the password and run the whole string through a hash function. Store the hash value and the salt. To verify the password, you rerun this process - append the salt, and apply the hash function. If the hashes match, you know your user entered the correct password, and as a bonus, your database doesn’t contain those passwords at all.
Not all hash functions are created equal - there are some specifically designed for password storage such as
Argon2id,scrypt,bcrypt, in this order of preference.
I'd avoid MD5 and SHA256 as well - you'll see why shortly.
Password Cracking Basics
Let’s do a quick and incomplete overview of password attacks:
- Brute-Force: trying all of the possible combinations. That’s what I am doing here. The slowest approach, but it’s simple to implement.
- Dictionary Attack: since passwords are often created by humans, we can restrict ourselves to known words and their combinations (and some variations). Much more efficient than the brute-force approach, but it’s harder to implement well.
- Password spraying: an honorable mention, instead of guessing the passwords you’d take a list of most common passwords and you’d find usernames that use them. Ridiculously effective, especially a variant that uses previously leaked passwords to these accounts from other sources. But I am getting distracted now.
Since I am using the brute-force approach I am arguing for an upper-bound cost of the attack as it’s the most time-consuming one of them.
There are generally two ways of brute-forcing passwords:
Online
You need to interact with the service (usually a webpage) to get information about password validity. You have many obstacles in your way:
- Calls over the network are “slow”: around 0.5s per password attempt is unacceptable for a large dataset,
- Lock-out policies: most sites implement a lock-out that temporarily stops you from attempting more passwords after several failed attempts. There are many ways of implementing this, from a hard block, through slowdowns to a captcha (another slowdown),
- Web Application Firewalls (WAFs): In this case, it’s more of the same - after several attempts you are no longer able to make guesses. Your IP might even get permanently blocked.
That being said - unless you somehow hack the site to get the user database for offline usage (or find it publicly available), you are condemned to this slow and risky approach.
Offline
It is also referred to as password cracking.
If somebody gave you a set of hashes and salts, you have greater options. No more networking, no more WAFs, you might do whatever you like. But reversing these hashes is still a tall order.
Since the use case for this is obvious (look at all these entries that need cracking!), there has been quite some progress in these methods and tools. The most significant speed leap was achieved by involving GPUs for computation - you need to do a lot of relatively parallel and relatively simple computations.
There are also highly performant tools for this process, taking advantage of the cutting-edge research: Hashcat and John the Ripper are the most famous. A side note: Argon2 is not yet supported in Hashcat - using it adds a nice layer of obscurity as "the best tool" is not able to crack these hashes right now.
If you have unsalted MD5/SHA1 or NTLM hashes (or perhaps others as well, these are the most common though), you migth try your luck with online databases that contain bilions of cracked passwords such as Crackstation, Onlinehashcrack and many others.
Renting GPUs and The Cost of Time
Calculating operating costs for a custom server with a lot of GPU cards (referred to as rig from now on) is complicated. It's much simpler to calculate renting costs for these rigs in big cloud companies such as AWS, Azure, or GCP.
In some cases (a single job you need to finish) it might even be a cheaper option than building a cracking rig on your own (+ a power plant required to operate it).
Benchmarks
You somehow need to figure out the rate of hashes you can go through in a second to get a feel of how costly is to try N options.
I have searched for a while and I was able to find somewhat recent benchmarks only for AWS. We thank Javy de Koning for the benchmarks - see repo.
As an example of how to read the benchmarks - take a look at the p5.48xlarge instance. There are 8 NVIDIA H100 80GB HBM3 GPUs and then we get a list of different hashes - the last line is the accumulated performance. I've picked the available previously discussed hashes for a somewhat short example. The following table is sorted by highest hash speed:
| Hash Mode | Hash Name | Total Hash Speed |
|---|---|---|
| 1000 | NTLM | 1496.2 GH/s |
| 0 | MD5 | 902.2 GH/s |
| 100 | SHA1 | 292.2 GH/s |
| 1400 | SHA256 | 126.9 GH/s |
| 1700 | SHA512 | 42293.4 MH/s |
| 3200 | bcrypt $2 | 2890.2 kH/s |
As you can see - there is a ~300000x speed difference between MD5 and bcrypt!
Then I stumbled upon these benchmarks from onlinehashcrack.com. Then I searched further, and I found a set of benchmarks from Chick3nman.
The idea right now is to get the data for the respective cards and search for rentable rigs that contain these cards. I need the data over time in a usable format - let's get coding.
Pricing
The second piece of the puzzle is the cost of renting the rigs.
Getting all of the data is technical busywork, not really that interesting for the purposes of this article. Nevertheless, you can find the source code here, and some comments below.
I am going to give kudos to Microsoft here - I found their pricing pages and docs easiest to use.
In Azure, they have the GPU optimized VMs, pricing.
Also, their lowest prices are spot prices - very cheap instances with interruptions. Hashcat can handle interruptions, and you are getting your notification - I am going for this option in the calculation.
Of course, there are other providers such as AWS and their Accelerated Computing EC2 instances. Or perhaps GCP's GPU Platforms, pricing. I just can't bring myself to deal with their pricing pages, and I suspect that the prices will not be different by an order of magnitude or four.
Disclaimer
I am fully aware that there are some differences between the benchmarked cards and the rentable cards (e.g. A100 benchmark with 40GB memory vs rentable A100 with 80GB memory). There are also missing benchmarks - the relevant VMs are just omitted. Science is hard and I am doing what I can (without spending a lot of cash to run the benchmarks).
Policy Complexity Calculations
So now we know how many dollars we are paying to try out N hashes. All that's left to do is a simple combinatoric exercise to determine how many hashes we need to go through to get a hash that complies with our desired policy.
At this point, let's not concern ourselves about the time costs - assume either that our cloud providers have a boundless supply of GPU rigs or that we are very, very patient.
Of course, the results below are generated by a script; find the script in the code repository.
Examples
Different Hashes with Password Length 8
Let's start with the most common policy known to me:
8 characters, including upper case, lower case, numbers and special symbols
(this set is referred to as ASCII printable sometimes).
Comparing several hashes mentioned earlier:
| Hashmode | Hash | Cracking price | |
|---|---|---|---|
| 0 | 0 | MD5 |
4.796$ |
| 1 | 10 | md5($pass.$salt) |
4.803$ |
| 2 | 100 | SHA1 |
13.689$ |
| 3 | 1000 | NTLM |
2.693$ |
| 4 | 1400 | SHA2-256 |
32.239$ |
| 5 | 3200 | bcrypt $2*$, Blowfish (Unix) |
3618932.102$ |
| 6 | 8900 | scrypt |
310683.001$ |
We can see the drastic difference between the recommended hashes and the "not recommended" hashes.
Nearly anybody can afford to crack the 8-character policy on weak hashes (MD5, SHA1, NTLM..), but you need a solid investment to try this approach on the better hashes such as
bcryptorscrypt.
As a side note, we can see that having the hashes with salt has pretty much the same time complexity. The benefit is in not having the hashes already cracked and widely available.
Another side note, there comes a point, when it's cheaper to buy and operate your own rigs. Even though it's not so simple with the shortages of GPUs.
Length vs Password Complexity
MD5 is still out there, so let's use that. Also, let's start examining the costs when increasing password lengths from 6. The same rules apply - using the ASCII printable character set, we can see that the price for the length of 8 matches the table above.
| Password length | Cracking price | |
|---|---|---|
| 0 | 6 | 0.001$ |
| 1 | 7 | 0.05$ |
| 2 | 8 | 4.796$ |
| 3 | 9 | 455.574$ |
| 4 | 10 | 43279.484$ |
| 5 | 11 | 4111550.983$ |
| 6 | 12 | 390597343.375$ |
| 7 | 13 | 37106747620.656$ |
| 8 | 14 | 3525141023962.341$ |
| 9 | 15 | 334888397276422.4$ |
We can see that the cracking price rises fast with every added character (yes, it's exponential growth). Maybe we can get away with a simpler approach; let's review the same MD5 hash with only lowercase letters:
| Password length | Cracking price | |
|---|---|---|
| 0 | 6 | 0.0$ |
| 1 | 7 | 0.0$ |
| 2 | 8 | 0.0$ |
| 3 | 9 | 0.004$ |
| 4 | 10 | 0.102$ |
| 5 | 11 | 2.653$ |
| 6 | 12 | 68.98$ |
| 7 | 13 | 1793.492$ |
| 8 | 14 | 46630.803$ |
| 9 | 15 | 1212400.875$ |
As we can see, even with a simple hash function, and a small character set, we can still create strong passwords by adding length. Related XKCD.
Still, for completeness sake, let's take a look at different character sets, MD5, length 12 (chosen to prove a point):
| Charset | Charset lenght | Cracking price | |
|---|---|---|---|
| 0 | numbers | 10 | 0.001$ |
| 1 | lowercase | 26 | 68.98$ |
| 2 | lowercase+uppercase | 52 | 282544.036$ |
| 3 | lowercase+uppercase+number | 62 | 2332095.31$ |
| 4 | ASCII printable | 95 | 390597343.375$ |
Including special characters does help. Moreover, it encourages the usage of password managers, but that's a topic for another article.
The Experiment
Since I am not bringing you an exhaustive list of cloud pricing comparisons, I decided to spice this article up by performing an Azure experiment to see how the calculations correspond to reality.
The plan
Azure grants you a 200$ free credit upon registration. Let's use it to spin some VMs.
The estimates are adjusted for the selected SKU (Standard_NC6s_v3, 3.953$/h) and don't reflect the cheapest option.
What I want to see is if we get the classic 8char policy on MD5 as well as a longer, but simpler MD5 policy. Then some comparisons in the SHA family with various hash lengths and one comparison to see the increase in costs with salt. Finally, let's see if we can get some scrypt cracks with a reduced length.
| Charset | Password Length | Hashmode | Full Policy Cost ($) | Full Policy Time (s) | Full Policy Time (h) | |
|---|---|---|---|---|---|---|
| 0 | ASCII printable | 8 | 0 | 129.6952 | 118113 | 32.8093 |
| 1 | lowercase only | 11 | 0 | 71.7533 | 65345.7 | 18.1516 |
| 2 | ASCII printable | 7 | 100 | 4.3534 | 3964.69 | 1.1013 |
| 3 | ASCII printable | 7 | 1400 | 9.9613 | 9071.79 | 2.51994 |
| 4 | ASCII printable | 7 | 1410 | 9.9531 | 9064.25 | 2.51785 |
| 5 | ASCII printable | 7 | 1700 | 31.8008 | 28961 | 8.04473 |
| 6 | ASCII printable | 5 | 8900 | 7.3646 | 6706.95 | 1.86304 |
| Sum | 264.8817 | 241227.38 | 67.00776 |
And we're over budget.
The invoice
Of course, once the hash is found, Hashcat refuses to burn the GPU anymore. We are searching only up to that point, so there is a probability it'd only take a fraction of the estimated time. The expected value is, of course, 50% of the time (assuming a completely random password distribution). Here are the expected values:
| Charset | Password Length | Hashmode | Exp Policy Cost ($) | Exp Policy Time (s) | Exp Policy Time (h) | |
|---|---|---|---|---|---|---|
| 0 | ASCII printable | 8 | 0 | 64.8476 | 59056.5 | 16.40465 |
| 1 | lowercase only | 11 | 0 | 35.8767 | 32672.85 | 9.0758 |
| 2 | ASCII printable | 7 | 100 | 2.1767 | 1982.345 | 0.55065 |
| 3 | ASCII printable | 7 | 1400 | 4.9807 | 4535.895 | 1.25997 |
| 4 | ASCII printable | 7 | 1410 | 4.9766 | 4532.125 | 1.25892 |
| 5 | ASCII printable | 7 | 1700 | 15.9004 | 14480.5 | 4.022365 |
| 6 | ASCII printable | 5 | 8900 | 3.6823 | 3353.475 | 0.93152 |
| Sum | 132.4409 | 120613.69 | 33.50388 |
You can also get lucky or unlucky - there's no saying beforehand where your concrete value would land. So, finally, I'll show you the measured results that I've got and the percentage of space it searched based on time estimates.
| Charset | Password Length | Hashmode | Real Cracking Time (s) | Real Cracking Time (h) | Searched Space (%) | |
|---|---|---|---|---|---|---|
| 0 | ASCII printable | 8 | 0 | 86617.0824 | 24.0603 | 73.33 |
| 1 | lowercase only | 11 | 0 | 36964.3600 | 10.2679 | 56.57 |
| 2 | ASCII printable | 7 | 100 | 2561.5532 | 0.7115 | 64.61 |
| 3 | ASCII printable | 7 | 1400 | 967.8948 | 0.2689 | 10.67 |
| 4 | ASCII printable | 7 | 1410 | 6618.8811 | 1.8386 | 73.02 |
| 5 | ASCII printable | 7 | 1700 | 1070.9561 | 0.2975 | 3.70 |
| 6 | ASCII printable | 5 | 8900 | 210.3699 | 0.0584 | 3.14 |
| Sum | 135011.0975 | 37.5031 | 55.97 |
So I got lucky where it didn't matter much and unlucky where it counted a lot. Oh well. The last cell is computed as a total percentage of searched space - the real time vs. the full projected time from the first table in this section.
And I can proudly present the invoice (in EUR, you can convert to USD):
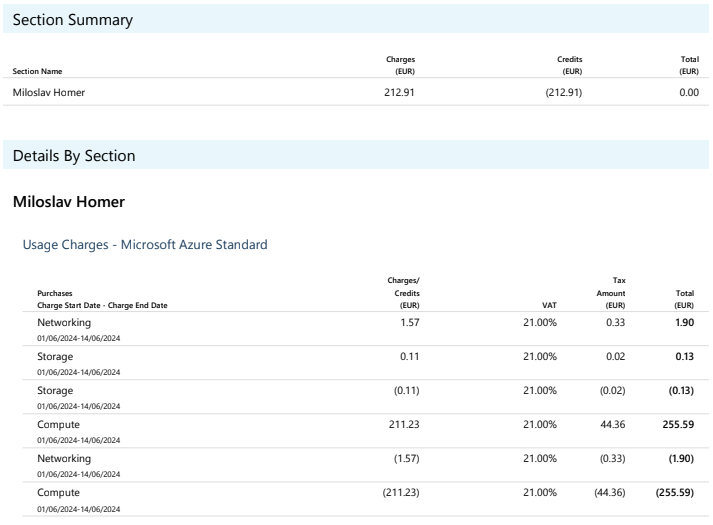
Of course I went overboard, I wasn't able to fully utilize the compute time due to testing/debugging and one misclick (ran an experiment overnight, but a wrong one, so I woke up to several hours of compute wasted).
Surprisingly, Microsoft covered the difference for me and I somehow got all of it accounted to credits. Thanks, Microsoft! One could even say, that I've got these hashes cracked for free. That's less than the original estimate of approx 10 USD, but now I am trolling hard. Nevertheless, keep in mind that hackers can replicate this method too, so any result under 200 USD could be thought about as free passes for hackers.
Ultimately, it was more fun than digging through AWS pricing and GCP pricing and probably simpler too!
Conclusion
Now you know how costly it could be for an attacker to break your password policy in the case of a hash leak. You might even be tempted to try it yourself - in that case: good luck with the cracking! I did, so you don't have to, but you can!
The biggest benefit is to use a tailored hash function (and salt!) such as Argon2id, scrypt or bcrypt; if you are not able to do that, then you need to use lengthier passwords (12 - 15 characters and more) with a diverse character set. Moreover, if your password has a length of 8 characters or less and it’s hashed with MD5 or SHA-*, consider it cracked immediately after it’s leaked.
Use a good policy that reflects the value of the asset you are protecting - your users needn't remember the passwords as they should use password managers, anyway.
Check out the code repository related to the article at https://github.com/ArcHound/password-policy-calculations.
